А вы знали, что Клод Шеннон, исследователь из Bell Labs и профессор инженерных наук MIT, придумал извлекать премию из волатильности раскоррелированных активов с помощью их сочетания в портфеле и ребалансировки ещё до Гарри Марковица, в 1940-х годах? Его мысленный эксперимент на эту тему назвали «демоном Шеннона», о чем и будет этот пост.
Кто такой Клод Шеннон? На этот счёт есть целый документальный фильм The Bit Player (2018), трейлер которого ниже. Скажем так, вы читаете этот пост на своем устройстве, потому что в 1916 году человечеству повезло, что Клод Шеннон родился.
Шеннон сделал то, что практически никто не делал со времён эпохи Возрождения – он единолично изобрёл новую важную область знаний. Его теория информации – абстрактное знание о коммуникации, на которой основаны компьютеры, интернет и всё цифровое.
Говорят, в истории так было всего несколько раз, чтобы кто-то один основал новую область знаний, задал все правильные вопросы, сам же на все из них ответил и доказал.
Тоби Бергер
Как пишет Паундстон в своей книге Fortune’s Formula, для описания влияния заслуг Шеннона на нашу современную жизнь сложно подобрать слова. Помимо всего остального, это он изобрёл те самые нули и единицы, биты. И цифровые схемы. Надо ли говорить, сколько всего это сделало возможным – от компьютеров и сетей до космических аппаратов и секвенирования ДНК.
Как сильно это повлияло на нашу жизнь?
Как изобретение алфавита на литературу.
Не повлияло, а определило.
Такой ум, как у Шеннона, остановиться на одной теме не мог. И одни из его интересных и малоизвестных наблюдений были сделаны как раз в области инвестирования, что нас тут и интересует. Речь о том, что впоследствии назвали демоном Шеннона.
В истории науки можно встретить много известных демонов, например, демона Декарта, Лапласа, Дарвина или Максвелла. Под демонами тут в каком-то смысле понимаются те самые сверхъестественные существа, способные изменять или искажать реальность. За это умение их используют в качестве мысленного эксперимента для описания каких-нибудь процессов, для непосвящённого человека выглядящих странно. Или чтобы продемонстрировать новую концепцию, как было с виртуальной реальностью у Декарта, демон которого вводил нас в заблуждение.
Что касается демона Шеннона, то он иллюстрирует то, как регулярная ребалансировка портфеля может приносить доходность, даже если активы в этом портфеле по отдельности никакой доходности не приносят. Словно из воздуха, а на самом деле из случайности (волатильности) и неидеальной корреляции. Иными словами, демон Шеннона – не что иное, как премия за ребалансировку.
Мысленный эксперимент, который Шеннон, согласно той же книге Паундстона Fortune’s Formula, придумал в 1940-х, был примерно следующим: представьте очень волатильный актив, который каждый день то удваивается в цене, то теряет половину своей стоимости (+100/-50%). Половину портфеля вы инвестируете в него, а вторую половину держите в наличных деньгах – здесь доходность всегда 0%.
Каждый день вы ребалансируете портфель обратно к распределению 50%/50%. Если в первый день стоимость актива, назовём его «акция», удваивается, вложенные в неё 500 /денег/ становятся 1000, а наличных у вас остаётся 500, стоимость портфеля к концу дня 1500. В начале следующего дня вы делите эти 1500 пополам и отправляете в «акцию» и наличные по 750, после чего стоимость «акции» падает вдвое, и у вас остаётся 375 в «акции» и 750 в наличных, стоимость портфеля равна уже 1125. Дальше всё повторяется.
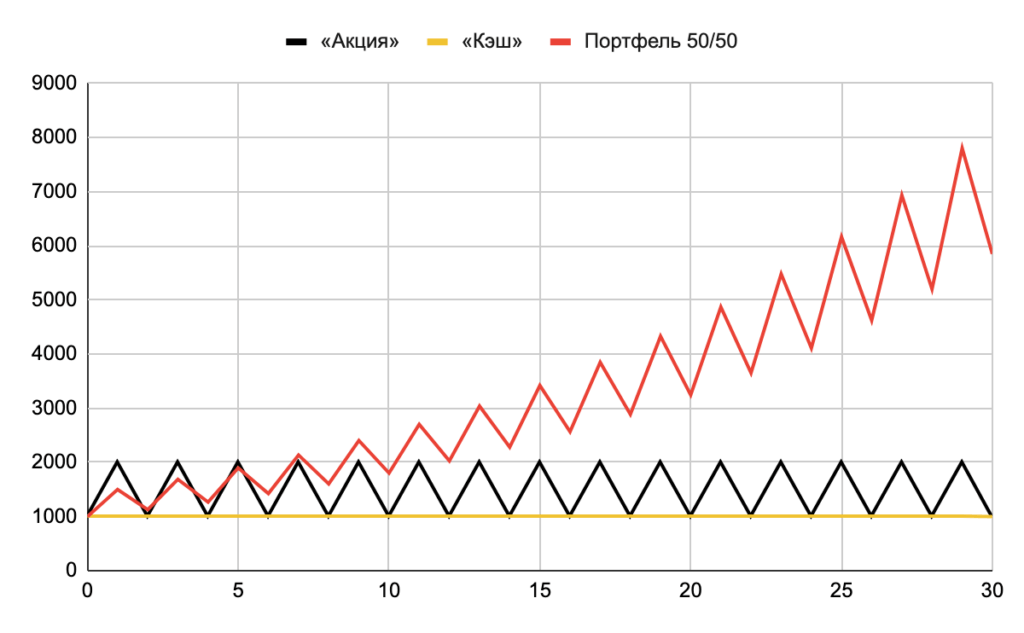
Как видно на графике эксперимента, ни один из «активов» сам по себе не растёт – спустя 30 периодов их стоимость осталась на изначальном уровне 1000. Средняя геометрическая доходность акции равна 0%. Но если объединить их в равновзвешенный (не обязательно) портфель и в каждом периоде или хотя бы иногда ребалансировать (обязательно), т. е. восстанавливать исходные доли «активов» в портфеле, продавая то, что выросло, и покупая то, что упало, то спустя 30 периодов мы получим почти в 6 раз больше денег, чем вложили в два «актива» с нулевой средней геометрической доходностью.
Что?! Откуда? Проделки демона Шеннона! 😉
Для простоты и большей наглядности я изобразил доходность «акции» как последовательно чередующуюся, у Шеннона доходность выбиралась из двух вариантов (+100% или -50%) броском монетки. Суть это не меняет, эксперимент работает и со случайным активом. В статье курса портфельный эффект я уже показывал, как два актива со случайно генерируемой доходностью и неидеальной корреляцией в одном портфеле с ребалансировкой дают больше доходности с меньшим риском, чем по отдельности. Это тоже была вариация демона Шеннона.
Интереса ради попробуем заменить «кэш» на «облигации», добавить третий актив «золото» и сделать паттерны доходности чуть ближе к реальности – акция будет со временем расти (+70/-35%), облигация будет расти медленнее (-5/+10%), а золото будет самым волатильным в этой тройке и с нулевым CAGR (+100/-50%). Равновзвешенный портфель из них по прежнему растёт быстрее, чем любой из отдельных «активов»:
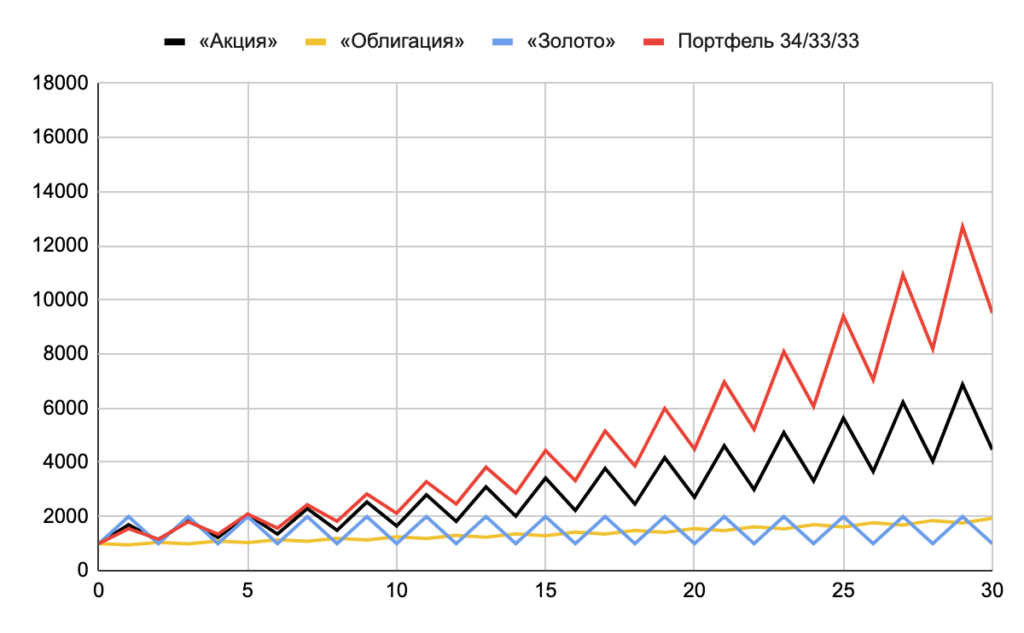
Корреляция между «активами» в этих неслучайных примерах из-за чередования доходностей получается значительно выше нейтральной (нулевой), в среднем около 0,5. Но в портфеле есть очень волатильные активы, и этого хватает, чтобы увидеть большую премию от ребалансировки.
Лучше всего демон Шеннона работает при соблюдении трёх ограничивающих его условий:
- Активы волатильные. И чем сильнее волатильность, тем лучше. Если рассматривать диверсифицированные классы активов, которые обычно добавляют в портфель, рассчитывая владеть ими долго, то они не так уж и волатильны. Акции или золото тут на первом месте, но как в примерах они скакать не будут, по крайней мере не каждый день. Это несколько ограничивает потенциальную премию.
- Активы обладают слабой (нейтральной) корреляцией. Ещё лучше – отрицательной. Шеннон в своём примере не просто так использовал кэш, его корреляция к случайному активу, доходность которого определяется броском монетки, нулевая. Реальных классов активов с устойчивой ±нейтральной корреляцией друг к другу не много, не говоря о сильной отрицательной (таких нет). Три основных всем известны – акции, облигации или кэш, золото или другие товары. Демон справится со всем, что не коррелирует на 100%, но чем выше корреляция, тем ниже премия.
- Ребалансировка дешёвая. Ещё лучше – бесплатная. Трансакционные издержки и налоги уменьшают премию. Этот факт и отсутствие гигантской дневной или месячной волатильности делает более оптимальной редкую ребалансировку, например, раз в год.
Вот так и получается, что истоки портфельной теории принадлежат айтишникам, а не финансистам, потому что Марковиц опубликовал свою легендарную статью Portfolio Selection только в 1952 году. Deal with it! 😃
В 40-х и 50-х годах прошлого века мир не был готов ко многим открытиям Шеннона, но со временем у человечества получилось ими воспользоваться в полной мере. Что касается его финансового открытия, оно остаётся не вполне понятым вплоть до сегодняшних дней. Да, мы научились строить портфели, но остаются области, в которых о ребалансировке только начинают говорить. Интересный пример – факторные премии. Согласно этой статье 2020 года, они являются лишь результатом ребалансировки. В других статьях diversification return, как называют дополнительную доходность от ребалансировки, объясняет значительную часть факторных премий. Тут есть о чём подумать.
Хотите научиться инвестировать? Пройдите обучающий курс о создании инвестиционного портфеля.
Нравится блог? Поддержите меня подпиской и получите доступ к преимуществам.