Монте-Карло симулятор: стресс-тест для ваших портфелей
Несколько интересно проведенных вечеров, и вот результат - новый инструмент для более продвинутого финансового планирования, который способен показать вам не один сценарий развития событий, как это обычно делается в классических личных финансовых планах, а тысячи! На основе его результатов можно сделать выводы о реалистичности вашего финплана.
Инструмент доступен здесь, но сначала немного теории. Когда вы составляете финансовый план, считая сколько вам надо откладывать, чтобы накопить нужную сумму, либо тратить, чтобы не потратить весь капитал раньше времени, обычно берется средняя ожидаемая доходность конкретного портфеля, то есть какая-то цифра из 50-го процентиля возможных исходов.
Это значит, что примерно половина всех исходов по доходности и результирующему капиталу будет меньше того, что представит вам такой план, а половина — больше. В составлении такого финансового плана нет ничего плохого — это полезное упражнение, да и цель его не только в том, чтобы показать какие-то конкретные цифры. Но стоит понимать, что в спектре всех исходов рассчитанный план является лишь одним из вариантов развития событий (пусть и наиболее вероятным).
Чтобы проанализировать гораздо большее число вариантов, используют метод Монте-Карло. Его суть заключается в генерации большого числа случайных исходов на основе входных параметров и последующем анализе их распределения, что позволяет наглядно представить спектр вероятных исходов и сделать более конкретные выводы о реалистичности заложенных инвестором в свой финансовый план параметров.
Есть разные подходы для генерации случайных исходов, подходящие для разных областей науки, где применяется такой анализ. После анализа исторических данных на ежегодных интервалах для этого инструмента я выбрал лог-нормальное распределение доходностей, потому что толстые концы кривой распределения на этих интервалах практически нивелируются. Если не уверены, что понимаете о чем речь, можно почитать пару моих статей про риск и распределение доходностей — будет легче разобраться с инструментом.
А теперь к практике. Мы разберем три примера использования инструмента.
Классический пенсионер
Многим известно знаменитое Trinity study, в рамках которого был проанализирован портфель из американских акций и облигаций (50/50) на 30-летних периодах с целью выяснить безопасную ставку ежегодного снятия средств (safe withdrawal rate, SWR). То есть такую, при которой портфель не исчерпал себя раньше конца 30-летнего периода.
Результатом были 4%, которые сегодня популяризированы в качестве rule of thumb и часто используются будущими пенсионерами для финансового планирования.
Возьмем теперь цель выйти на пенсию с $1000 (я буду использовать 70 000 руб.) и представим, что есть план по её достижению, основанный на правиле 4%, то есть итог накопления по этому плану будет 70000 * 12 / 0.04 = 21 000 000 руб. Его реалистичность мы и будем проверять.
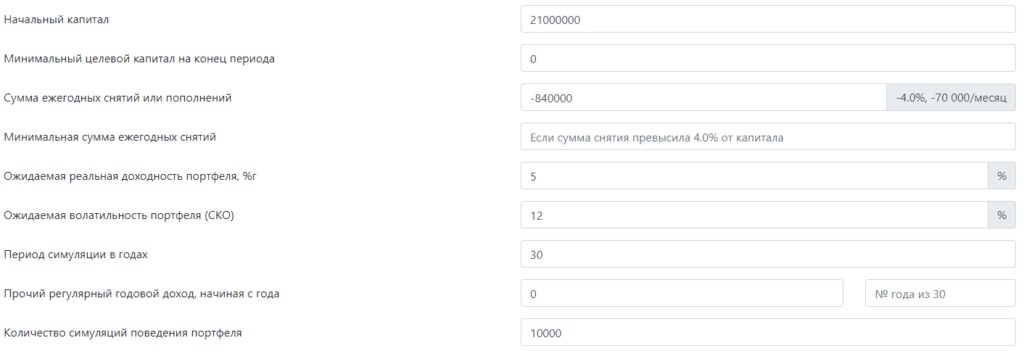
В качестве минимального целевого капитала вводим 0, потому что цель — не проесть все деньги за 30 лет. Для финансового планирования удобно использовать реальную доходность, то есть за вычетом инфляции, потому что это позволяет вводить все суммы в сегодняшних деньгах и освобождает разум от прогнозов инфляции. Допустим, что реальная средняя геометрическая (CAGR) доходность портфеля этого инвестора 5%. В качестве ожидаемой волатильности (СКО) портфеля возьмем 12%. Остальные поля пока не трогаем.
На основе этих данных инструмент сгенерирует 300 000 случайных годовых доходностей (10 000 раз по 30 лет), то есть вместо исторических сотен лет для анализа у нас будет несколько сотен тысячелетий, вместо одного портфеля и 30-летнего периода — 10 000.
Вот результаты из моего запуска (каждый раз они отличаются, но чем больше повторений, тем идентичнее результаты между запусками):
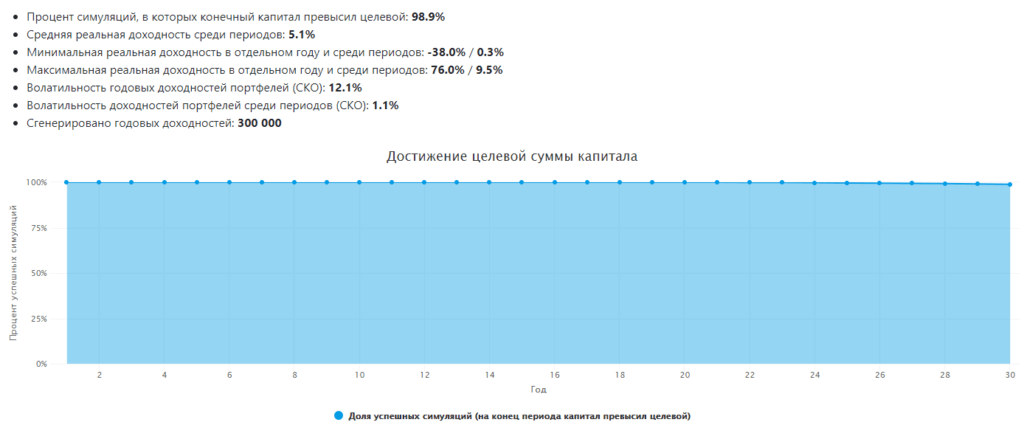
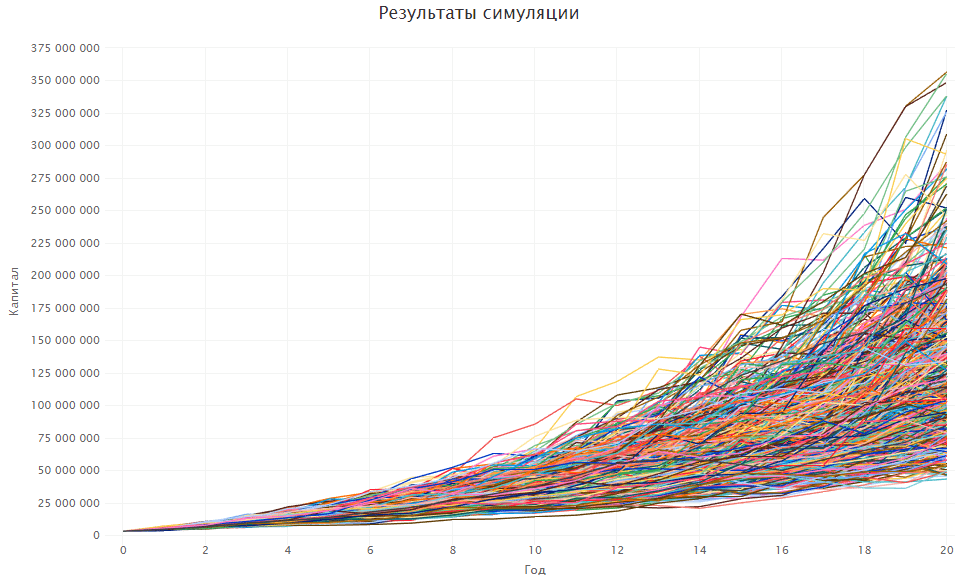
Это лишь основная часть результатов — запустите симулятор сами, чтобы посмотреть остальные графики.
В таком сценарии и при условии, что мы допускаем трату всего капитала (в целевую сумму мы ввели 0), всё обещает быть отлично. При реальной средней доходности портфеля в 5% годовых результаты Trinity study вполне подтверждаются.
Но что если мы обязательно хотим сохранить капитал? Тогда вместо нуля в поле целевого капитала можно ввести начальный. В этом случае конечные суммы в каждом из 10 000 полученных портфелей будут сравниваться не с нулем, а с указанным целевым капиталом.
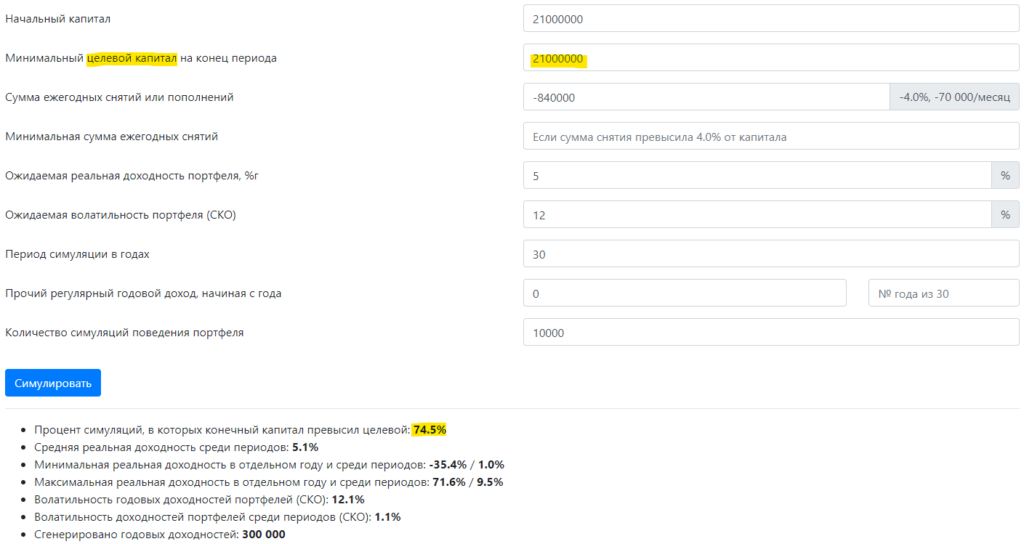
И тогда вместо 99% мы получим гораздо менее обнадеживающие 75% — шанс не выполнить цель на сохранение капитала становится значительным. Но не все так плохо. Такой процент успешных симуляций — это то, с чем можно поработать. Как?
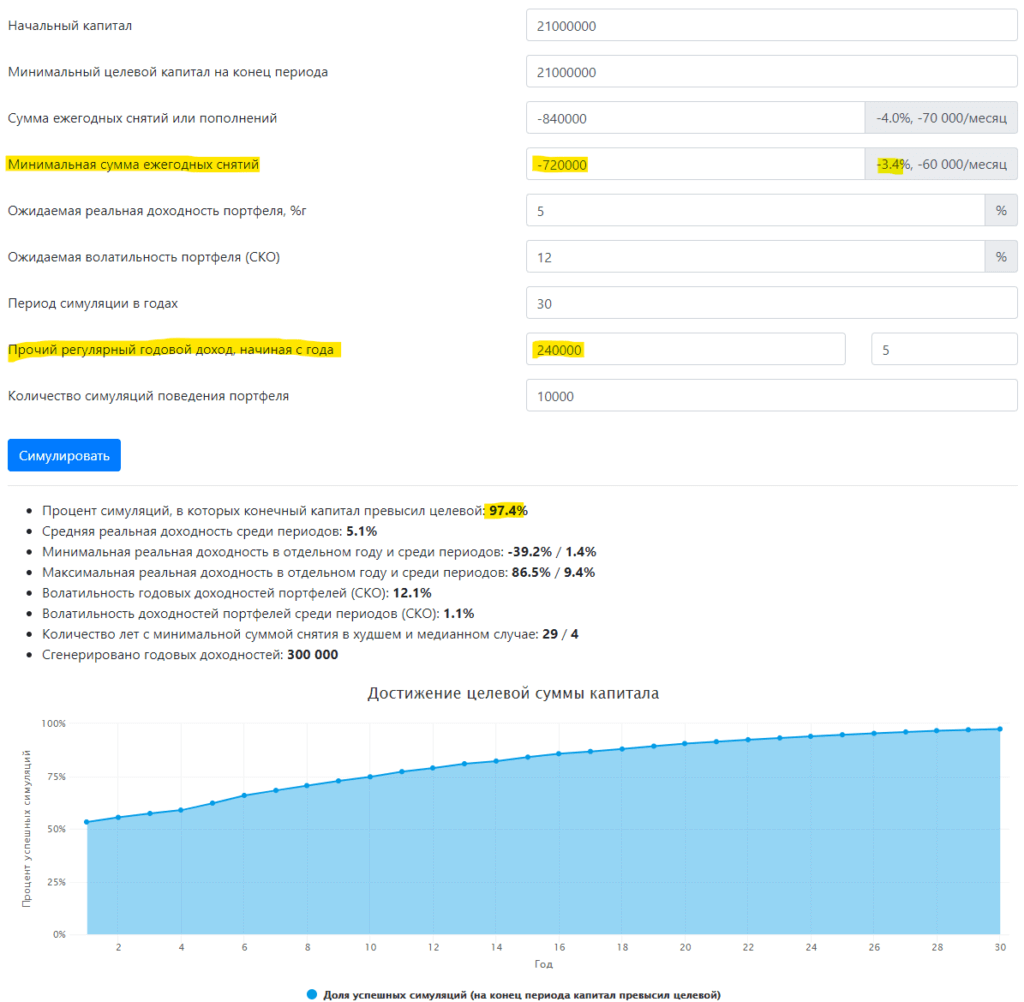
Во-первых, в худые годы наш инвестор может ужаться и перестать слепо вытягивать из портфеля проиндексированные на инфляцию 840 000 рублей в год. Вместо них будет 720 000 рублей, то есть 60 000 в месяц. На эту сумму наш пенсионер начинает жить, если обычная сумма снятия начинает превышать запланированную долю в 4% от текущего размера портфеля.
Во-вторых, государство будет платить ему шикарную пенсию в 20 000 рублей (тоже индексируется на инфляцию), начиная с 5-го года его 30-летнего периода свободы, а это нелишние 240 000 рублей сегодняшних денег в год для наших расчетов.
Как видно из результатов, ситуация выправляется — 97% портфелей закончили этот путь с балансом больше нуля. В медианном случае 4 года из 30 инвестору придется удовлетвориться уменьшенным снятием средств, чтобы увеличить шансы своего портфеля на существование. В худшем случае на уменьшенной пенсии придется сидеть 29 лет, но вероятность этого довольно низкая. В 90% случаев это будет 15 лет или меньше.
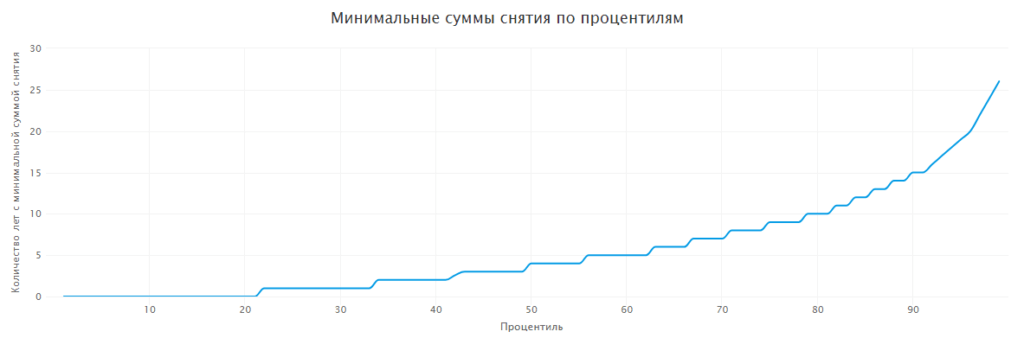
Таков основной принцип работы с инструментом. Теперь коротко пройдемся по остальным сценарием.
Ранний пенсионер
Сегодня популярность набирает идея финансовой независимости и раннего выхода на пенсию (FIRE). Инвестиционный горизонт у таких инвесторов расширяется до 50–60 лет, с чем связана основная проблема — 4% в чистом виде становятся заметно опаснее (есть ряд исследований, показывающих это на реальных и сгенерированных доходностях).

Я ввел такие же данные, как в самый первый раз, но заменил 30 лет на 60 и указал целевой капитал, равный начальному, потому что смотреть как таят деньги на счете, осознавая, что до конца пенсии ещё лет 30, сможет не каждый. Вместо 99% мы получили 83%, что довольно рисково, хотя и нельзя сказать, что судьбу нашего раннего пенсионера может решать монетка.
Давайте внесем похожие коррективы в этот гениальный план:
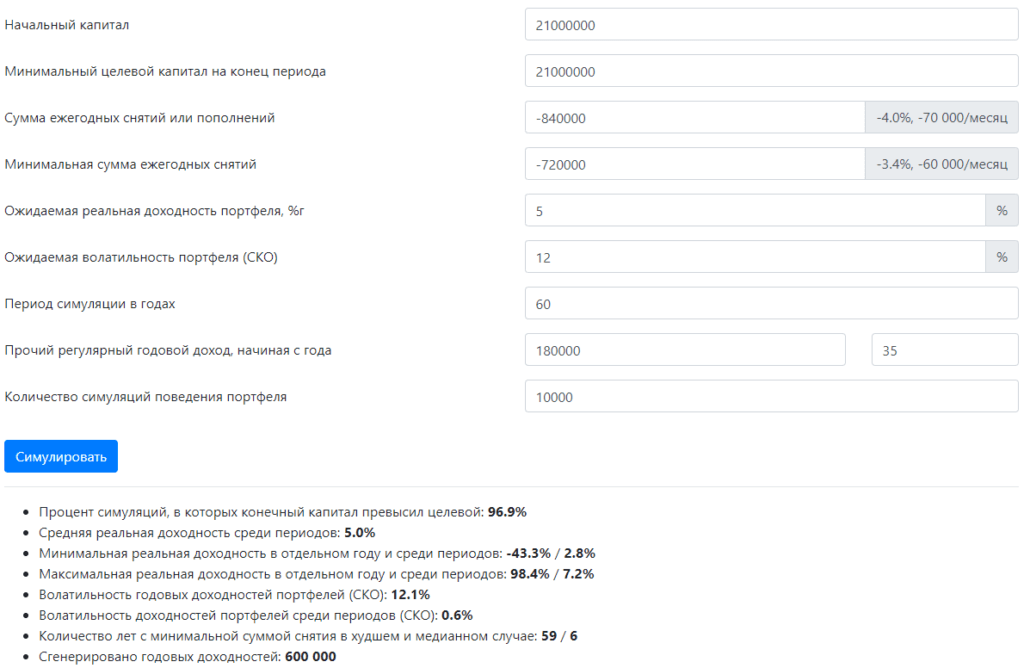
Годы тренировок по скоростному накоплению денег позволят нашему пенсионеру ужиматься при необходимости до 60 000 руб. в месяц, а на 35 году году пенсии государство начнет выплачивать ему 15 000 руб. в месяц.
В результате получаем статистически надежные 97% с почти той же медианой на минимальном потреблении в 10 лет и до 29 лет с минимальной суммой снятия в 90% всех случаев.
Когда я смогу накопить?
Напоследок рассмотрим как использовать инструмент для анализа не трат, а накоплений. Возьмем того же раннего пенсионера, который планирует накопить 21 000 000, откладывая по 2 000 000 в год и имея начальный капитал в миллион. Параметры будут такие:
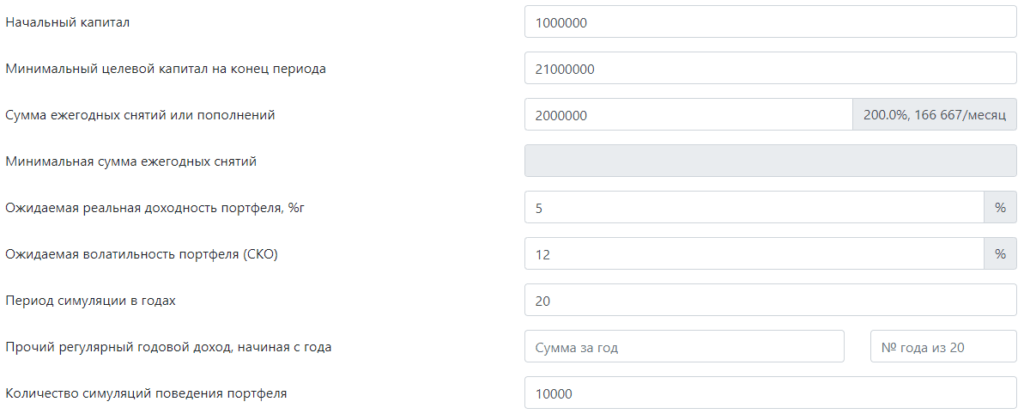
Вместо отрицательной суммы снятий указываем положительную, означающую пополнение. Период симуляции ставим с запасом, чтобы посмотреть как меняется кривая:
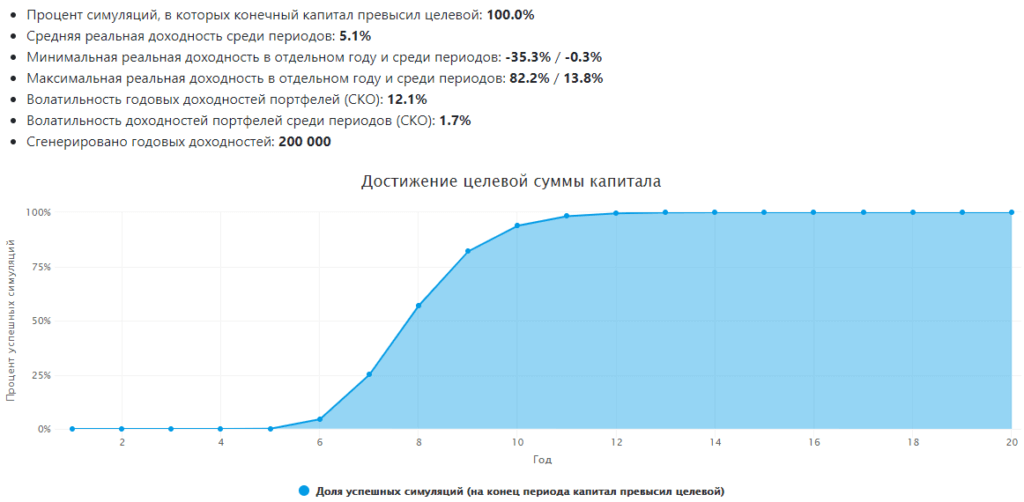
Обычный финансовый план, использующий среднюю доходность портфеля для расчетов, предскажет нам срок около 8 лет, что в симуляторе означает процент успешности около 50%.
Ценной здесь является информация о худшем случае, то есть на каком году процент успешности превысит психологически комфортный для вас порог этого плана (например, 80%) или принятые в статистике за надежные 95%.
В этом примере надежным ориентиром выглядит срок в 10–11 лет, которые понадобятся, чтобы собрать достаточный капитал, если дела на рынке пойдут хуже среднего. Такой подход позволяет уточнить границы сроков накопления и подготовить себя психологически к реализации не самых лучших сценариев. С другой стороны, в случае везения нужную сумму можно собрать за 6–7 лет.
Напишите в комментариях считаете ли новый инструмент полезным и будет ли вам интересно уточнить свои ожидания по срокам накопления и ставкам снятия средств?
P.S. Благодарю Андрея Болкисева за помощь с добавлением в модель возврата к среднему, что приблизило распределение генерируемых доходностей к реальному рынку (историческим данным по акциям США и всего мира).
Комментарии
Спасибо вам большое, за ваш труд!
Очень интересно. Будет чем занят несколько дней. Огромная благодарность за работу!
Спасибо, интересная математика!
Очень хорошо дополняет возможности созданного ранее "Финансового плана" - возвращает с небес на землю, напоминая, что спланированные результаты могут реализоваться к нужному времени далеко не всегда. Большая благодарность автору!
Дмитрий, большое спасибо! Подскажите, пожалуйста, вы используете какой-то веб-фреймворк для создания подобных инструментов и вывода графической информации?
Это клиентские SPA на React, для графиков используется Highcharts. Серверная часть есть только у инструмента анализа портфелей (написана на Golang).
Подскажите по модели возврата к среднему, какую использовали - на основе отрицательной автокорреляции, или на основе модели Орштейна-Уленбека? Как вычислили конкретные показатели возврата к среднему для американского и мирового рынка? На основе показателя Хёрста? (т.е. грубо говоря что СКО за период T вырастает не до T^0,5, а с некоторым понижающим коэфф. a^ln(t)*T^0,5 Укажите, плз, параметры - сейчас аналогичную модель делаю.
Прежде всего моделирование делалось на годовых данных, которых в этом случае достаточно - это его сильно облегчило. В части возврата к среднему там просто добавляется множитель на основе предыдущих элементов сгенерированного ряда, который немного "пружинит" его к среднему, так что можно сказать на основе отрицательной автокорреляции. Показатель Хёрста не считался, вместо этого сверялось распределение исторических и сгенерированных доходностей по процентилям.
множитель на основе предыдущих элементов сгенерированного ряда - на сколько глубоко смотрит в историю (день, месяц, год)? Или берет все элементы с долей, убывающей например обратно пропорционально времени T или T^0,5 или ln(T)? Если в целом, то сколько это сжатие составило на годовых СКО? Т.е. например до этого множителя СКО был 20%, а стал 17% - т.е. какой коэфф. сжатия примерно?
Берет все элементы и использует количество прошедших лет. СКО всегда примерно равно введённому ожидаемому, а возврат к среднему действует на цену. Если нужны подробности, напишите в телеграме (в био канала есть мой юзернейм).
Дмитрий, я не понимать, поясните плиз: Вы рассматриваете такой пример при симулировании "раннего пенсионера": "Я ввел такие же данные, как в самый первый раз, но заменил 30 лет на 60 и указал целевой капитал, равный начальному, потому что смотреть как таят деньги на счете, осознавая, что до конца пенсии ещё лет 30, сможет не каждый. Вместо 99% мы получили 83%" Получается, когда мы ставим 60 лет, капитал не проедается до уровня "0" в 83% случаев, изначально было 99% (при 30 годах). Вывод: при увеличении срока , вероятность сохранения капитала снижается с 99 до 83%. Но!!! если я ставлю минимальный целевой капитал на конец периода не "0", а "21.000.000", то при симуляции на 30 лет: конечный капитал превысил целевой в 73,6%. Затем 30 лет ---> 60 лет, симуляция: конечный капитал превысил целевой в 82,3%. Вывод : при увеличении срока, вероятность сохранения капитала УВЕЛИЧИВАЕТСЯ с 73,6 до 82,3%. Здесь нет противоречия?
> Получается, когда мы ставим 60 лет, капитал не проедается до уровня «0» в 83% случаев В 83% случаев капитал не проедается не до уровня 0, а до уровня начальной суммы. По второй части противоречия я не вижу, это просто значит, что капитал до нуля все-таки не опускается и стратегия достаточно устойчива, потому что чем больше времени проходит, тем большее количество разных исходов, первоначально опустившись ниже целевой суммы, успевают вернуться к ней. То есть при таких настройках чем больше вы поставите лет, тем выше будет процент достижения цели. Другими словами большинство изначально неудачных исходов восстанавливаются, не успев опуститься до нуля, то есть капитал после просадки отрастает. Можете воспринимать это как "включение в работу" сложного процента со временем.
Блин, я так долго строил в Экселе симуляции портфелей и пытался сделать анализ финансового плана, но здесь это просто табличка из моей мечты) Я часа 4 сидел безвылазно в плане и симуляторе, высчитывая все варианты своей финансовой жизни. Огромное спасибо за проделанную работу! Плюс описание VTBX и разбор странного индекса "нетто" в безналоговом фонде - бесконечно благодарен!)
Дмитрий, как у вас получается построить ломанные кривые на графике (которые при симуляции отображаются серым цветом), а не ровно-экспоненциальные? Может у вас есть эксель-файл с примером?
Серые кривые отображают случайно сгенерированные ряды данных с годовыми доходностями, то есть это N массивов доходностей за M лет, всего N * M точек на графике (показываются только 100 * M - все рисовать слишком дорого и бесполезно). Ровно-экспоненциальными они не могут быть, потому что являются случайными значениями из логнормального распределения с заданными параметрами.
Спасибо, суть понял) Правда пока не понял, как это реализовать в экселе и можно ли это сделать в нём вообще, ввиду такого количества данных.
В экселе можно генерировать такие ряды. Пример для логнормального распределения:
LOGNORM.INV(RAND(),LN(1+A1),A2)-1, где A1 - средняя геометрическая (это важно) доходность, A2 - стандартное отклонение. На выходе % случайной доходности или, если убрать -1, разы изменений. Только у меня ещё есть симуляция небольшого возврата к среднему, подогнанная под реальные рыночные данные, это уже сложнее сделать (без неё несколько пессимистичнее будут результаты).Распределение доходностей с выбором нужного процентиля - эт я умею строить, а вот множество промежуточных графиков в заданном коридоре неопределённости - нет) Мне понравилось, как они добавляют наглядности графику у вас на сайте. Но спасибо за пояснения) Симулятор отличный)