Инвестиционные игры
Эд Торп изобрёл стратегию игры в блэкджек - метод, известный сегодня как «подсчёт карт». Впервые я узнал об Эде в колледже, когда мы с друзьями провели одно лето в местных казино, пытаясь скопировать его методы подсчёта карт (у меня тогда получилось не очень). Несколько месяцев назад, исследуя жизнеспособность моей инвестиционной стратегии, я узнал, что он также является успешным инвестором.
Это мой перевод оригинальной статьи Investing Games из блога Breaking the Market.
Позже, работая профессором математики, мистер Торп заинтересовался инвестициями и в конечном итоге основал хедж-фонд. На протяжении почти 20 лет его хедж-фонд приносил 19% годовых всего с 3 убыточными месяцами. Результаты настолько феноменальны, что я почти сомневаюсь в их точности [позже был и второй фонд, но оба уже давно закрыты — прим. перев.]. Меня привлекли идеи мистера Торпа, они перекликаются с моими и также исходят из опыта за пределами инвестиционного мира. В одном из интервью он утверждает, что «понимание азартных игр — одна из лучших тренировочных площадок для входа в мир инвестиций» (49:30–58:20)». Я согласен.
В этом свете я предлагаю вам следующие игры, демонстрирующие философскую основу моей стратегии. Игры намеренно преувеличены и упрощены, чтобы подчеркнуть суть логики.
Игра №1
Ставите $100. Подбрасываете монету, орёл — выигрываете 50% от суммы ставки (получаете $150, прибыль $50), решка — теряете 40% своих денег (получаете $60, убыток $40). Сыграете?
| Раунд 1 | Формула | Выплата |
|---|---|---|
| Орёл | $100*150%= | $150 |
| Решка | $100*60%= | $60 |
| Среднее= | $105 |
Эта игра в вашу пользу. Шанс получить 150$ (выиграть 50$) составляет 50%, как и шанс получить 60$ (проиграть 40$). Ожидаемый результат — выигрыш $5 за игру, в среднем вы выигрываете. Большинство людей эту игру понимают и большой процент людей согласны играть.
Игра №2
Теперь давайте добавим нюанс. После первого раунда игра повторяется со всей выплатой первого раунда. Вы можете играть столько раз, сколько пожелаете, но каждый раз вы должны ставить всё. Пример:
«Вы начинаете игру со $100 и выигрываете первый раунд. Теперь у вас есть $150. Вы снова играете, внося ставку $150 и выигрываете второй раунд, теперь у вас $225. Вы снова играете с $225 и проигрываете в третьем раунде, у вас остаётся $135. Вы решаете остановиться».
Сыграете в эту игру? Она немного отличается от первой.
Если играете,
когда остановитесь?
Игра №3
Эта игра такая же, как и предыдущая, с той лишь разницей, что я решаю, когда игра закончится, а не вы. Вы поставите $100, и игра будет повторяться с выплатой за каждый прошлый раунд, пока я не решу остановиться. Играем?
Подумайте хорошенько, в чем отличия этих игр.
Правильный ответ, на мой взгляд, никогда не играть. Вы будете терять всё почти каждый раз. На самом деле, если позволить игре продолжаться вечно, игра всегда будет иметь тенденцию к полному проигрышу.
Странно, не правда ли? Игра работает в вашу пользу, если сыграть один раз, и против вас, если её повторить.
Повторяющиеся азартные игры имеют совсем другие шансы на успех, чем одноразовые. Результаты серии ставок, особенно серии умножений, определяются средним геометрическим значением и стремятся к нему. Одиночные ставки или группа одновременных ставок, в частности, серия сложений, рассчитываются по среднему арифметическому. Среднее арифметическое для игры составляет $1.05 на вложенный доллар, как видно из игры №1. Среднее геометрическое для игры №3 составляет sqrt(1.5*0.6) = $0.949 — потеря более 5% за игру.
Давайте рассмотрим пример для ясности. Играя в игру дважды, можно получить следующие возможные результаты:
| Раунд 1 | Раунд 2 | Формула | Выплата |
|---|---|---|---|
| Выигрыш | Выигрыш | $100*1.5*1.5= | $225 |
| Выигрыш | Проигрыш | $100*1.5*0.6= | $90 |
| Проигрыш | Выигрыш | $100*0.6*1.5= | $90 |
| Проигрыш | Проигрыш | $100*0.6*0.6= | $36 |
| Среднее= | $110.25 |
На первый взгляд, игра все ещё усредняется в вашу пользу, но уже можно видеть, что в 3 из 4 случаев вы получаете меньше $100, теряя деньги. Наиболее вероятные результаты — одна победа и одно поражение: 150% x 60% = 90%. Убыток 10%. Все понимают, что игра с подбрасыванием монеты со временем будет иметь тенденцию к равному распределению между орлом и решкой (по закону больших чисел), таким образом со временем игра имеет тенденцию приносить убыток.
Давайте посмотрим на игру из 20 попыток:
| Число выигрышей | Итоговый результат | Вероятность |
|---|---|---|
| 20 | $332,525.67 | 0.00% |
| 19 | $133,010.27 | 0.00% |
| 18 | $53,204.11 | 0.02% |
| 17 | $21,281.64 | 0.11% |
| 16 | $8,512.66 | 0.46% |
| 15 | $3,405.06 | 1.48% |
| 14 | $1,362.03 | 3.70% |
| 13 | $544.81 | 7.39% |
| 12 | $217.92 | 12.01% |
| 11 | $87.17 | 16.02% |
| 10 | $34.87 | 17.62% |
| 9 | $13.95 | 16.02% |
| 8 | $5.58 | 12.01% |
| 7 | $2.23 | 7.39% |
| 6 | $0.89 | 3.70% |
| 5 | $0.36 | 1.48% |
| 4 | $0.14 | 0.46% |
| 3 | $0.06 | 0.11% |
| 2 | $0.02 | 0.02% |
| 1 | $0.01 | 0.00% |
| 0 | $0.00 | 0.00% |
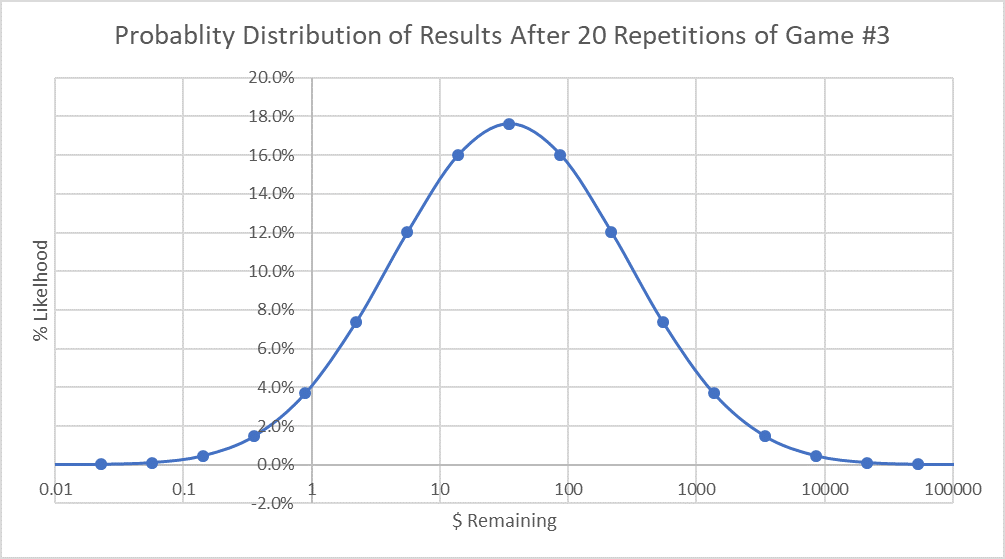
По вертикальной оси — вероятность, по горизонтальной — итоговая сумма.
Среднее по-прежнему положительное, но вероятность потерять деньги 75%. Наиболее вероятным исходом является убыток $65. В 40% случаев вы уйдёте с суммой меньше $14. Повторение ставок привело к сильному перекосу результатов в худшую сторону — большому проценту проигравших и небольшому количеству победителей (симметричным график делает логарифмическая шкала).
Сыграв 100 раз, вы с вероятностью 86% потеряете деньги и с вероятностью 54% получите меньше $1. Игра теперь больше похожа на лотерейный билет — небольшой шанс на хороший выигрыш и высокий шанс проиграть почти всё. Чем больше повторений, тем ближе процент проигрыша приближается к 100%.
Несколько счастливчиков станут неприлично богатыми, но большинство разорятся. Играть в эту игру со $100 не безумие, но стали бы вы играть, поставив 10% своего капитала? 50%? Назвал бы кто-нибудь этот тип игры «инвестицией»? Я бы не стал.
Это странное явление, и для его полного понимания может потребоваться некоторое время. Каждая игра с отрицательной геометрической доходностью со временем стремится к убыткам, даже если имеет положительную доходность в отдельном раунде. Тот же эффект происходит с менее волатильными играми (например, если орёл приносит выигрыш 4%, а решка — проигрыш 3,9%), только требуется больше повторений, чтобы эффект проявился.
Теперь спросите себя, понимают ли люди, инвестирующие ваш капитал, эту концепцию? Инвестируете ли вы в какие-то «лотерейные билеты»?
Игра №4
Правила как в игре №3, только в каждой игре ставка составляет $100. На всю игру у вас есть $10,000. Играете?
Вы повторяете игру, что в свете предыдущей игры должно заставить задуматься. Однако предыдущая выплата не переносится на следующий раунд. Каждый раунд стоит ровно $100. Таким образом, выигрыш и проигрыш являются аддитивными, а не мультипликативными, как в играх 2 и 3. Когда игра складывает и вычитает выигрыши и проигрыши, в дело вступает среднее арифметическое, а оно в вашу пользу на $5 за игру (см. игру №1). Поэтому вы должны играть.
Это игра, о которой думает большинство людей, когда они думают об игре №3.
Итак, что стоит усвоить отсюда? Игры, в которых выигрыши и проигрыши складываются, с большей вероятностью будут прибыльными, чем игры, в которых выигрыши и проигрыши умножаются. Ожидаемая доходность этих игр ближе к среднему арифметическому, а не к среднему геометрическому (среднее геометрическое всегда меньше среднего арифметического). Ключевое отличие этой игры от игры №3 заключается в том, что вы ограничиваете сумму своей ставки.
Игра №5
Начинаете со $100 и играете по тем же правилам, что и в игре №3, но на этот раз вы сами решаете, какой процент от вашей выплаты будет поставлен в следующем раунде. Я все ещё решаю, когда закончить. Играете? Пример:
«Вы начинаете игру со $100 и выигрываете первый раунд. Теперь у вас есть $150. Вы играете снова и решаете поставить $120 и выигрываете второй раунд, теперь у вас $210 ($120 * 1.5 + $30). Вы играете снова и решаете поставить $80, проигрываете в третьем раунде, у вас осталось $178 ($80 * 0,6 + $130). Я решаю остановиться».
Игра №3 очень убыточная, и эта игра очень на неё похожа. Она тоже мультипликативная и определяется отрицательным средним геометрическим.
Однако, если ставить правильные суммы, в игру №5 стоит играть. Держите свои ставки ниже 50% от общей суммы денежных средств на счёте, и вы будете склонны выигрывать деньги. Держите свои ставки на уровне 25% от депозита для максимизации выигрышей, зарабатывая 0,6% за игру.
В итоге:
- Игра №3 - на все деньги — гарантированные убытки.
- Игра №5 - на часть денег — вероятные небольшие выигрыши.
Так что же здесь произошло? С денежным «буфером» в 75% от ваших средств вы ограничиваете эффект отрицательного среднего геометрического и увеличиваете эффект положительного среднего арифметического. Фактический профиль игры такой:
| Выигрыш | Проигрыш | ||||
|---|---|---|---|---|---|
| Под риском | Кэш | Результат | Под риском | Кэш | Результат |
| 25%*150%+ | 75%= | 112.5% | 25%*60%+ | 75%= | 90% |
| Среднее геометрическое = (112.5% * 90%)1/2 = 100.62% |
Положительное среднее геометрическое! Вы можете играть в эту игру целый день и быть уверенными, что результаты сложатся в вашу пользу!
Эта концепция очень мощная. Размер вашей ставки изменяет долгосрочные результаты игры.
Игра №6
Те же правила, что и в игре №5, за исключением того, что одновременно идут две игры, и вы сами решаете, сколько инвестировать в каждую из них. Как играть здесь?
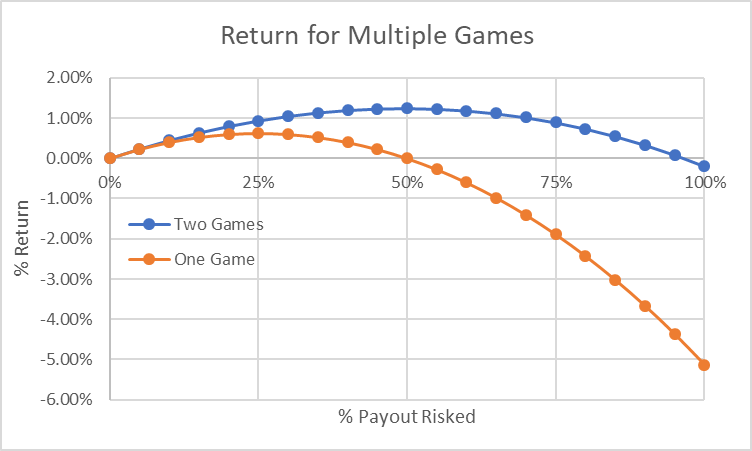
По вертикальной шкале доходность, по горизонтальной — размер ставки в % от имеющихся денег.
Ставить 25% на первую игру и 25% на вторую. Ребалансируйте ставки после каждого раунда, чтобы всегда ставить 25% денег на каждую из игр. Эта стратегия даёт среднее геометрическое 101,24% за игру. Диверсификация по двум одновременным играм увеличивает геометрическую доходность по сравнению с одной игрой, хотя среднее арифметическое по-прежнему равно 1,05. Чем больше одновременных игр, тем доходность ближе к средней арифметической.
Игра №7
Те же правила, что и в игре №6 с двумя играми одновременно, за исключением того, что вы можете решить, сколько инвестировать в каждую из игр только в самом начале. В каждом следующем раунде ставится вся выплата предыдущего. Как играть?
Никак. Игра такая же, как и №3, за исключением того, что две игры идут одновременно. Каждая в конечном итоге будет вести к убытку. Старт с двумя играми замедлит процесс деградации, но со временем он всё же происходит. Ребалансировка уберегает эти игры от коллапса.
Универсальная природа математики
Как говорилось ранее, игры преувеличены и намного проще, чем в мире инвестирования. Однако математика есть математика независимо от масштаба и сложности. Те же принципы, что и в этих семи играх, существуют в среде риска/доходности любой инвестиции. Долгосрочные результаты определяет среднее геометрическое. Размер ставки будет влиять на долгосрочные результаты. Ребалансировка увеличивает среднее геометрическое. Итак, давайте подумаем о различных популярных инвестиционных стратегиях применительно к этим играм.
- Какая игра представляет «купи и держи»?
- Какая игра представляет индексное инвестирование?
- Какая игра/ы представляют традиционное портфельное инвестирование?
- Какая игра/ы представляют следование тренду (trend following)?
- Какая игра представляет геометрическую балансировку? [стратегию, которую придумал для себя автор — прим. перев.]
- Какая игра представляет лучшую стратегию?