Интуитивное руководство по экспоненциальным функциям и числу e
e меня всегда волновала - не буква, а математическая константа. Что она на самом деле значит?
Это мой перевод статьи An Intuitive Guide To Exponential Functions & e из блога BetterExplained. Статья раскрывает суть числа Эйлера и экспоненциального роста (сложного процента). В процессе её чтения вы поймёте, что это была одна из самых полезных статей по финансам в вашей жизни. По крайней мере, у меня было именно так.
Книжки по математике и даже моя любимая Википедия описывают e, используя максимально непонятный жаргон:
Математическая константа e — это основание натурального логарифма.
Смотришь что такое натуральный логарифм, а там:
Натуральный логарифм, ранее известный как гиперболический логарифм, представляет собой логарифм по основанию e, где e — иррациональная константа, приблизительно равная 2,718281828459.
Классная циклическая ссылка. Определение корректное, но не очень-то полезное. И дело не в Википедии — многие математические объяснения выходят сухими и формальными в своем стремлении к строгости. Но это не помогает новичкам разобраться в предмете (а мы все когда-то были новичками).
Довольно! Сегодня я поделюсь своим интуитивным, высокоуровневым пониманием того, что такое число е и что в нём крутого. Оставьте свою скрупулёзную книжку по математике на другой раз.
e — не просто число
Описывать e как «константу, приблизительно равную 2,71828…» — все равно что называть Пи «иррациональным числом, приблизительно равным 3,1415…». Да, это правда, но вы полностью упустили суть.
Пи — это отношение между длиной окружности и диаметром, разделяемое всеми окружностями. Это фундаментальное соотношение, присущее всем кругам, и потому влияющее на любой расчет длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т. д. Число Пи важно и показывает, что все круги связаны, не говоря уже о тригонометрических функциях, производных от кругов (синус, косинус, тангенс).
e — это базовая скорость роста, разделяемая всеми непрерывно растущими процессами. e позволяет вам взять простой темп роста (где все изменения происходят в конце года) и найти влияние сложного (compound), непрерывного роста, когда каждую наносекунду (или быстрее) вы понемногу растете.
e появляется всякий раз, когда системы растут экспоненциально и непрерывно: население, радиоактивный распад, расчеты процентного дохода и многое другое. Даже системы, которые не растут плавно, можно аппроксимировать с помощью е.
Так же, как любое число может рассматриваться как масштабированная версия 1 (базовая единица), каждый круг можно рассматривать как масштабированную версию единичного круга (радиус 1), и каждый темп роста можно рассматривать как масштабированную версию e (единица роста в идеальных условиях).
Так что е — не какое-то невразумительное и случайное на первый взгляд число. e представляет идею о том, что все постоянно растущие системы являются масштабируемыми версиями общего темпа роста.
Понимание экспоненциального роста
Давайте начнем с рассмотрения простой системы, которая удваивается через некоторое время. Например:
- Бактерия может делиться и «удваивается» каждые 24 часа
- Мы получаем в два раза больше лапши, когда складываем её пополам.
- Ваши деньги удваиваются каждый год, если вы получаете доходность в 100% (счастливчик!)
И выглядит это так:
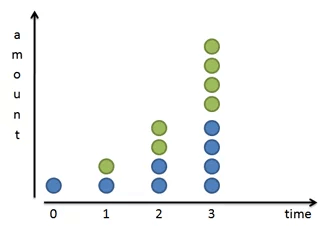
Расщепление пополам или удвоение — очень распространенная прогрессия. Конечно, можно и утраивать, и учетверять, но удвоение удобнее, так что рассмотрим его подробнее.
Математически, если у нас есть x таких расщеплений, то мы получим в 2x раз больше чего бы то ни было по сравнению с начальным количеством. С одним расщеплением у нас будет в 21 или в 2 раза больше. После 4 расщеплений получится в 24 = 16 раз больше. Общая формула выглядит так (growth = рост):
Говоря иначе, удвоение — это рост на 100%. Мы можем переписать нашу формулу так:
Это то же уравнение, но в нём мы делим число 2 на части, из которых оно действительно состоит: исходное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить вместо 100% любое число (50%, 25%, 200%) и получить формулу роста для этой новой ставки. Итак, общая формула для x периодов получения доходности (return):
Всё это просто означает, что мы используем наш коэффициент роста, (1 + return), x раз.
Более внимательный взгляд
Наша формула предполагает, что рост происходит дискретными шагами. Наша бактерия ждёт, ждёт, а затем бум, и удваивается в самую последнюю минуту. Наш процентный доход волшебным образом появляется на отметке в 1 год. Основываясь на приведенной выше формуле, рост является прерывистым и происходит мгновенно. Зеленые точки появляются внезапно.
Мир не всегда работает так. Если мы увеличим масштаб, то увидим, что наши бактериальные друзья делились постепенно:
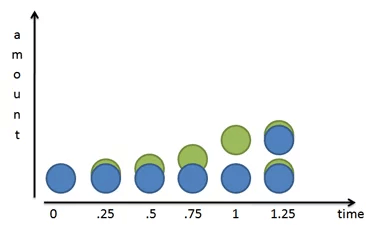
Мистер Грин не появляется просто так: он медленно вырастает из мистера Блю. Через 1 единицу времени (в нашем случае 24 часа), мистер Грин оказывается завершен. А затем он становится зрелой голубой клеткой и может создавать новые собственные зеленые клетки.
Меняет ли эта информация наше уравнение?
Нет. В случае с бактериями неготовые зеленые клетки не могут ничего делать пока не вырастут полностью и не отделятся от своих синих родителей. Уравнение всё ещё в силе.
Деньги меняют всё
С деньгами всё иначе. Как только мы заработаем цент процентами, этот цент может начать зарабатывать свои микро-центы. Нам не нужно ждать, пока мы заработаем полный доллар процентами — новые деньги не нуждаются в зрелости.
Исходя из нашей старой формулы, процентный рост выглядит так:
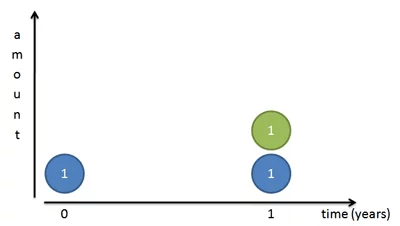
Но опять же, это не совсем верно: все проценты внезапно появляются в последний день. Давайте увеличим масштаб и разделим год на две части. Мы зарабатываем 100% годовых каждый год или 50% каждые 6 месяцев. Таким образом, мы зарабатываем 50 центов в первые 6 месяцев и еще 50 центов во второй половине года:
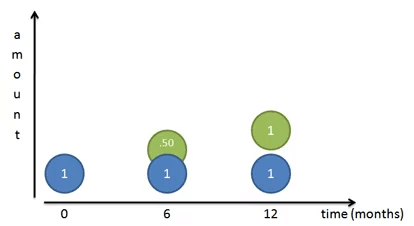
Но и это неправильно! Конечно, наш первоначальный доллар (мистер Блю) приносит доллар в течение года. Но спустя 6 месяцев у нас уже были готовые к использованию 50 центов, которыми мы пренебрегли! Эти 50 центов могли заработать собственные проценты:
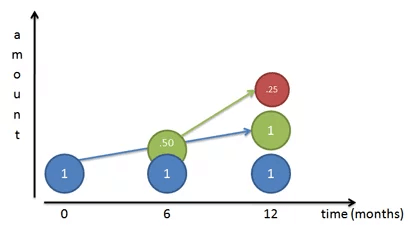
Поскольку наша ставка составляет 50% за полгода, эти 50 центов принесли бы ещё 25 центов (50% × 50 центов). В конце первого года у нас были бы:
- Изначально вложенный доллар (мистер Блю)
- Доллар от мистера Блю (мистер Грин)
- 25 центов от мистера Грина (мистер Рэд)
Итого $2,25. От нашего первоначального доллара мы получили $1,25, что даже лучше, чем удвоение!
Обратим нашу доходность в формулу. Рост на двух полу-периодах на 50% выглядит так:
Погружение в сложный процент
Время идти дальше. Вместо того, чтобы делить рост на два периода по 50%, давайте разделим его на 3 сегмента по 33%. Кто сказал, что нам нужно ждать 6 месяцев, прежде чем мы начнем получать проценты? Это даст нам такой график:
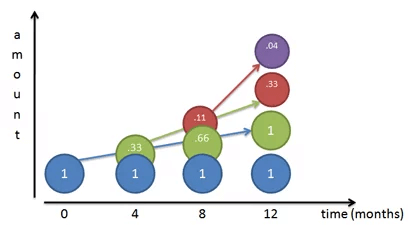
- Месяц 0: Мы начинаем с мистера Блю — $1.
- Месяц 4: Мистер Блю заработал на себе 1/3 доллара и создал мистера Грина стоимостью в 33 цента.
- Месяц 8: мистер Блю зарабатывает еще 33 цента и передает их мистеру Грину, теперь тот стоит 66 центов. Мистер Грин заработал 33% от своей предыдущей стоимости, создав 11 центов (33% × 33 цента). Эти 11 центов становятся мистером Рэд.
- Месяц 12: Мистер Блю зарабатывает еще 33 цента и передает их мистеру Грину, теперь тот стоит полный доллар. Мистер Грин заработал 33% прибыли от своей предыдущей стоимости в 8 месяце. Он передает эти 22 цента (33% × 66 центов) мистеру Рэду, который теперь стоит 33 цента. А мистер Ред, начавшийся с 11 центов, заработал на себе 4 цента (33% * 0,11), создав мистера Пёрпл.
Фух! Окончательная стоимость спустя 12 месяцев составила: 1 + 1 + 0,33 + 0,04 = 2,37.
Постарайтесь действительно понять что происходит здесь с ростом:
- Каждый цвет зарабатывает проценты и передает их другому цвету. Вновь созданные деньги могут зарабатывать деньги сами по себе, и этот цикл продолжается.
- Мне нравится думать, что исходная сумма (мистер Блю) никогда не меняется. Мистер Блю копит деньги, чтобы создать Мистера Грина, стабильные 33 цента каждые 4 месяца, поскольку мистер Блю не меняется. На диаграмме у мистера Блю есть синяя стрелка, показывающая как он подкармливает мистера Грина.
- Так уж выходит, что Мистер Грин создает и тоже кормит мистера Рэда (зеленая стрелка), но мистер Блю об этом не знает.
- По мере того, как мистер Грин растет (его постоянно кормит мистер Блю), он все больше и больше помогает расти мистеру Реду. Между 4 и 8 месяцами мистер Грин дает мистеру Реду 11 центов. Между 8 и 12 месяцами уже 22 цента, поскольку мистер Грин тоже растёт. Если мы расширим диаграмму, мистер Грин даст мистеру Рэду 33 цента, потому что к 12 месяцу он достиг полного доллара.
Разобрались? Поначалу это непросто — я даже немного запутался, когда составлял графики. Но обратите внимание, что каждый доллар создает себе маленьких помощников, которые, в свою очередь, создают помощников себе и так далее.
Используя 3 периода в нашем уравнении роста, мы получаем формулу:
Мы заработали $1,37, даже больше, чем $1,25 в прошлый раз!
Можем ли мы получить бесконечные деньги?
Почему бы не взять еще более короткие периоды времени? Как насчет каждого месяца, дня, часа или даже наносекунды? Будет ли наша прибыль взлетать до небес?
Рост и правда становится лучше, но только до определенного момента. Попробуйте подставить разные числа вместо n в нашей волшебной формуле, чтобы увидеть общую прибыль:
n (1 + 1/n)^n
———————————-
1 2
2 2.25
3 2.37
5 2.488
10 2.5937
100 2.7048
1,000 2.7169
10,000 2.71814
100,000 2.718268
1,000,000 2.7182804
…Числа становятся больше и сходятся примерно в 2,718. Эй… подожди-ка… это похоже на е!
В гиковых математических терминах e определяется как темп роста, если мы постоянно начисляем 100% доходности на всё меньших и меньших периодах времени:
Данная последовательность сходится, чему есть доказательства. Но, как видите, с уменьшением периодов времени общая доходность остаётся около 2,718.
Но что всё это значит?
Число e (2,718…) — это максимально возможный результат начисления 100% роста за один период времени. Конечно, вы изначально ожидали роста с 1 до 2 (это на 100% больше, не так ли?). Но с каждым крошечным шагом вы создаете небольшие дивиденды, которые начинают расти сами по себе. В конце концов вы получите e (2,718…), а не 2. e — это максимум или то, что происходит, когда мы начисляем 100% на вложенный капитал так часто, как только возможно.
Итак, если мы начнем с $1,00 и постоянно начисляем доходность по ставке 100%, мы получаем 1e. Если мы начнем с $2,00, то получим 2е. Если начнем с $11,79, то получим 11,79e.
Число e похоже на ограничение скорости (как c — скорость света), говорящее насколько быстро вы можете расти, используя непрерывный процесс. Возможно, вы не всегда достигаете предела скорости, но это ориентир: любой темп роста можно записать с помощью этой универсальной константы.
(Примечание: будьте осторожны, отделяя прирост от конечного результата. 1, становящаяся e (2,718…) — это прирост на 171,8% (темп роста). e, само по себе, является конечным результатом, который вы наблюдаете после того, как весь рост будет учтён (изначальное значение + увеличение)).
Что насчёт разных ставок?
Хороший вопрос. Что, если мы будем расти на 50% в год вместо 100%? Можем ли мы по-прежнему использовать е?
Посмотрим. Темп роста в 50% будет выглядеть так:
Хм. Что мы здесь можем сделать? Помните, что 50% — это общая доходность, а n — количество периодов, на которые её нужно разделить при начислении сложного процента. Если мы выберем n = 50, мы можем разделить нашу ставку на 50 частей по 1%:
Конечно, это не бесконечность, но масштаб довольно мелкий. А теперь представьте, что мы так же разделили нашу обычную ставку 100% на части по 1%:
Так, что-то появляется. В уже привычном случае у нас есть 100 накопленных изменений по 1% каждое. В сценарии с 50% у нас есть 50 накопленных изменений по 1% каждое.
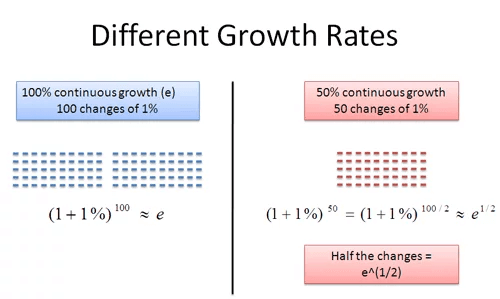
Слева: 100% непрерывный рост (e) — 100 изменений по 1%.
Справа: 50% непрерывный рост — 50 изменений по 1%.
Половина изменений = e ^ 1/2
В чем разница между этими двумя числами? Ну, второе — это просто половина количества изменений:
Это весьма интересно. 50 / 100 = 0,5 — показатель степени, в которую мы возводим е. И это работает в общем случае: если бы у нас был темп роста 300%, мы могли бы разбить его на 300 изменений по 1% каждое, то есть в три раза больше при темпе e3.
Несмотря на то, что рост может выглядеть как сложение (+1%), мы должны помнить, что на самом деле это умножение (x1,01). Вот почему мы используем экспоненты (возведение в степень, многократное умножение) и квадратные корни (означают «половину» числа изменений, то есть половину числа умножений).
Хоть мы и выбрали 1%, мы могли бы выбрать любую небольшую единицу роста (0,1%, 0,0001% или даже бесконечно малое число!). Ключ в том, что для любой ставки, которую мы выберем, это просто новый показатель степени е:
Что насчёт разных периодов?
Предположим, что рост по ставке в 300% продолжался 2 года. Тогда годовой рост (e3) следуют умножить на себя, то есть возвести во вторую степень:
И в общем случае (rate = ставка и time = период времени):
Благодаря магии экспонент мы можем избежать двух степеней и просто перемножить ставку и период в одном показателе степени.
Большой секрет: e объединяет ставку и период времени
Это круто! ex может означать две вещи:
- x — это сколько раз мы умножаем темп роста: 100% годовых за 3 года = e3
- x — это сам темп роста: рост на 300% за год = e3
Не сбивает ли это совпадение с толку? Перестанут ли работать наши формулы и наступит ли конец света?
Всё сходится. Когда мы пишем ex, переменная x представляет собой комбинацию ставки и периода.
Позвольте объяснить. Когда речь идёт о непрерывном начислении сложных процентов, 10 лет роста по 3% в год имеют такое же конечное влияние, как и 1 год 30% роста (и никакого последующего).
- 10 лет роста по 3% означают 30 изменений по 1%. Эти изменения происходят в течение 10 лет, поэтому вы растете непрерывно на 3% в год.
- 1 период 30% роста означает 30 изменений по 1%, но происходящих в течение одного года. То есть вы растете на 30% в год и останавливаетесь.
В каждом случае происходят одни и те же «30 изменений по 1%». Чем выше ваша ставка (30%), тем меньше времени вам понадобится для того, чтобы добиться того же эффекта (1 год). Чем ниже ваша ставка (3%), тем дольше вам нужно расти (10 лет).
Но в обоих случаях рост в конечном итоге равен e0,3 = 1,35. Мы нетерпеливы и предпочитаем большой и быстрый рост маленькому и медленному, но e показывает, что они оба варианта имеют тот же чистый эффект.
Итак, наша общая формула выглядит так:
Если у нас есть доходность r на t периодах времени, наш чистый рост с учётом сложного процента составит ert. Кстати, это работает даже для отрицательной и дробной доходности.
Пример: максимальные процентные ставки
Предположим, что у меня есть $120 на счете с 5%-ной ставкой. Мой банк щедр и дает мне максимально гранулярное начисление сложного процента. Сколько денег у меня будет через 10 лет?
Наша ставка составляет 5%, и нам повезло, что она начисляется непрерывно. Через 10 лет получаем 120 x e0,05 x 10 = 197,85. Конечно, большинство банков не настолько учтивы, чтобы давать вам лучшую возможную частоту начислений процента. Разница между вашей фактической и непрерывной доходностью есть величина, на которую вы не нравитесь банку.
Что дальше?
Узнайте о близнеце экспоненты — натуральном логарифме.
Комментарии
Интересно. Выходит, если среднегодовая реальная доходность моего портфеля составляет 5% и я держу его 20 лет, то покупательная способность денег, инвестированных в этот портфель увеличится в е раз.
Верно для идеальных условий, 0,05 * 20 = 1, e^1 = e.
Просто класс! Если б мне так преподавали, я бы стал экономистом, а не инженером)
Вряд ли. В статье разбирается "максимально гранулярное начисление сложного процента", а 5% среднегодовой доходности это обычный сложный процент. Поэтому будет формула сложного процента и рост в 2.65 раза. Мое ошибочное мнение.
В облигациях - да, а вот на счет акций не уверен - всё же компании зарабатывают свою прибыль постоянно, и внутри них она реинвестируется под сложный процент снова и снова. Может быть, в акциях мы и получаем что-то ближе к e. Что-нибудь вроде (1 + 1 / 365) ^ 365 = 2,714...
Как они работают внутри - не важно. Важно лишь, как мы их считаем. Если 5% в вопросе это все приращение по итогам каждого года, то экспоненциальный процент роста будет 4.88. Я это к тому, что каждый раз, когда пишут процент роста, надо понимать, по какой формуле этот процент считается. Иначе ответы будут разные.
Ну да, если цена уже изменилась на 5%, то больше ждать неоткуда) Но априорное отличие между акциями и облигациями в этом плане должно быть.
Весьма познавательно! Но пока не сложилось как применить это на практике.
если вложить 1 копейку или 1 цент под 3 % годовых на 2000 лет ,то будет 47 на 10 в 22 степени .Для сравнения бюджет России 10 в 12 степени .Почему так ни кто не разбогател ?Да просто ничего в природе не растет вечно! На этом ужение Дарвина построено ,там размножение слонов рассматривалось ( они медленно размножаются 22 месяца беременность вроде) Если бактерии так удваиваются ,как тут описано весьма за короткое время ,они сравняются не то что с массой земли ,а с массой солнца !!! Да чего то такое не наблюдается ,вот почему надо предпочесть Дарвина ,а не Баффетта и прочих экономистов .Их теории гроша ломанного не стоят .Рост с постоянной скоростью ,приведет к бесконечности .А если вы видите бесконечность в своей теории ,значит теория не верная :)
Картинки с формулами не загружаются
Спасибо, поправил.
Федор, как получили значение 4,88?
Дмитрий, доброго дня Одно дело размножаться, другое дожить до момента размножения. Если слоны размножаются делением и в t=0, у нас 100 слонов, то по математике в t=2, слонов у нас 200. А в реальности 50 слонов съели папуасы. И в t=2 у нас опять 100. Если копейка вложена на 2000 лет, то кто её за это время спас от деноминации, захвата, отжима, кутежа и растраты, похищения НЛО? Риск на таком сроке легко отъест набранный копейкой жирок. Вопрос про копейку аналогичен вопросу «неужели за всю человеческую историю еще не напроизвели денег на всех человеков? Как же так? Куда деньги деваются тогда» ИМХО